在電路理論中,疊加定理作為分析線性電路的關鍵原理,為解決復雜電路問題提供了高效且系統的方法。以下將從其定義、使用步驟、適用范圍及局限性等方面,深入闡述這一重要定理。
一、疊加定理的定義
疊加定理指出,在線性電路中,任一支路的電流(或電壓)等于電路中各獨立電源分別單獨作用于該電路時,在該支路產生的電流(或電壓)的代數和。這里的 “激勵” 即為獨立源,包括電壓源和電流源等;“響應” 則指電路中某一支路或元件上的電壓或電流。
二、正確使用疊加定理的步驟
確定電路中各變量的參考方向,這將決定變量前的符號,為后續計算提供方向依據。
逐一畫出獨立源單獨作用時的等效電路圖。當某一獨立源單獨作用時,其他不作用的獨立源需置零,具體方法為:不作用的電壓源用短路代替,不作用的電流源用開路代替。
在每個等效電路中,分別求出對應的待求變量。
最后,將各獨立源單獨作用所得結果進行代數疊加,得到最終的響應結果。
三、疊加定理的適用范圍與注意事項
疊加定理具有一定的適用范圍和使用條件,必須嚴格遵循以下原則:
僅適用于線性電路 :線性電路的特性是元件的伏安特性呈線性關系,如線性電阻、理想電感和電容等。這是疊加定理成立的基礎前提,而非線性電路則不適用。
受控源的處理 :若線性電路中含有受控源,在使用疊加定理時,應將受控源作為一般元件始終保留在電路中,不能像獨立源那樣置零處理。
功率計算的特殊性 :由于功率與電壓和電流呈非線性關系(P=I²R 或 P=U²/R),因此不能直接運用疊加原理來計算功率,這是疊加定理的一個重要局限性。
四、為什么疊加定理僅適用于線性電路
以電阻為例,可清晰闡釋這一問題。
(一)線性電阻與非線性電阻的區別
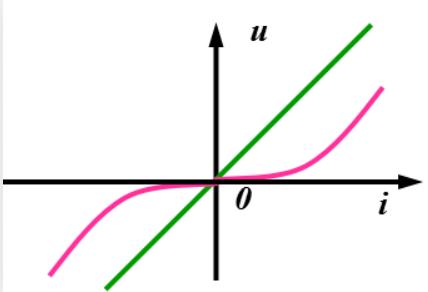
從伏安特性曲線來看,線性電阻表現為一條過原點的直線,直線上各點的斜率(即電阻值)保持恒定;而非線性電阻的伏安特性曲線則是一條曲線,如半導體二極管的伏安特性曲線,曲線上各點的斜率(電阻值)隨外加電壓和電流的變化而變化。

(二)電壓疊加時電流的變化情況
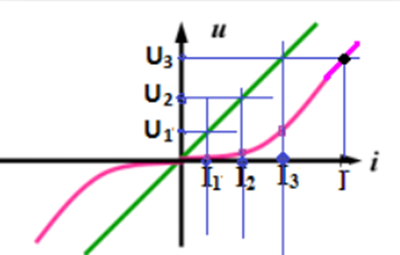
假設電阻為線性電阻,阻值恒為 R。當分別施加電壓 U? 和 U? 時,根據歐姆定律可得對應的電流 I?=U?/R 和 I?=U?/R;當同時施加電壓 U? 和 U?(即總電壓 U?=U?+U?)時,電流 I?=(U?+U?)/R=I?+I?,明顯符合疊加原理。
然而,若電阻為非線性電阻,情況則截然不同。同樣分別施加電壓 U? 和 U? 時,對應的電流為 I?=U?/R? 和 I?=U?/R?;而當總電壓 U?=U?+U? 加到該電阻上時,由于非線性電阻在不同電壓下的阻值不同(R?≠R? 和 R?),此時電流 I?=(U?+U?)/R?≠I?+I?,疊加原理在此不再成立。
(三)伏安特性曲線的直觀體現
從伏安特性曲線上也可直觀觀察到,僅當元件的伏安關系呈線性(如綠色線)時,才有 I?=I?+I?。而非線性元件(如紅色線),當電壓為 U?=U?+U? 時,電流 I 不等于 I?+I?,進一步驗證了疊加定理僅適用于線性電路的特性。
〈烜芯微/XXW〉專業制造二極管,三極管,MOS管,橋堆等,20年,工廠直銷省20%,上萬家電路電器生產企業選用,專業的工程師幫您穩定好每一批產品,如果您有遇到什么需要幫助解決的,可以直接聯系下方的聯系號碼或加QQ/微信,由我們的銷售經理給您精準的報價以及產品介紹

〈烜芯微/XXW〉專業制造二極管,三極管,MOS管,橋堆等,20年,工廠直銷省20%,上萬家電路電器生產企業選用,專業的工程師幫您穩定好每一批產品,如果您有遇到什么需要幫助解決的,可以直接聯系下方的聯系號碼或加QQ/微信,由我們的銷售經理給您精準的報價以及產品介紹
聯系號碼:18923864027(同微信)
QQ:709211280


